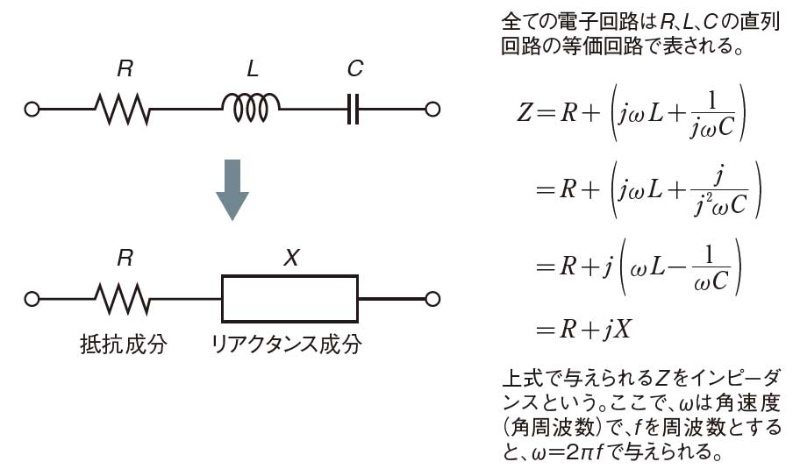
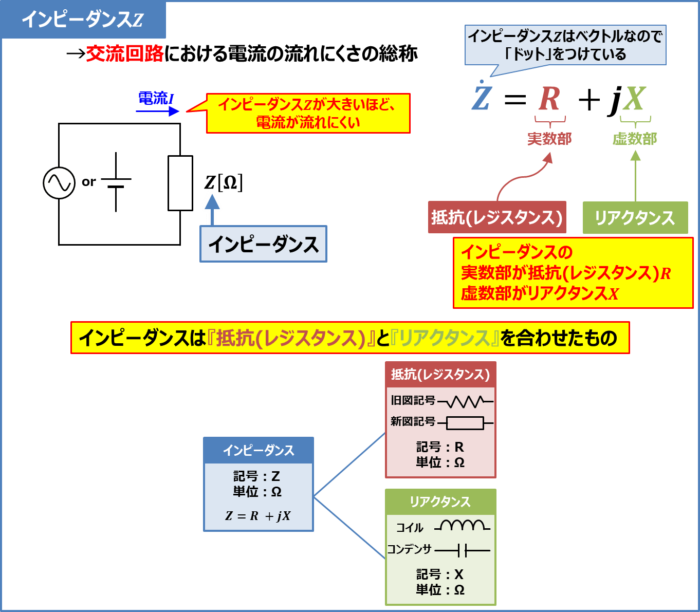
インピーダンスや共振を理解して アンテナ設計のポイントを押さえる 日経クロステック Xtech
自己誘導 はコイルに流れる電流が変化すると、コイルに自己誘導起電力(逆起電力)が発生する現象です。 自己誘導起電力の向きは電流の変化を妨げる向きとなります。 上図において、抵抗\(R\)の値や電圧源\(E\)の値を変えることによって、コイルに流れる電流\(I\)を変化させると、磁束鎖交数しかし、電荷が コイルを通過 するときの電圧降下は熱エネルギーと関わりがありません。 注目したいのは、 コイルに電流が流れるとコイル内に磁場が生まれる という点です。 実はこれ、エネルギーの1つの形なのです。コイルの空間中に磁場が存在することは1つのエネルギーであり、 磁場の
コイル 電圧 公式
コイル 電圧 公式-交流電源 交流回路とは, 電源装置の起電力が常に正であるような直流回路とは異なり, 電源装置の起電力が時間的に正負に振動しながら変化する電源装置を含んだ回路のことをあらわす その中でも高校物理の議論の対象となるのは, 次式のように正弦波の形 解決済 500回巻きで、コイルの断面積が4センチ×4センチ、磁石が96mステラ、中心が960ガウスです。 このコイルの中で、磁石を回転させて発電します。 1，1秒間あたりの回転数によって発生する電圧は、理論的にはどのようにかわるのでしょうか。 計算
インピーダンスや共振を理解して アンテナ設計のポイントを押さえる 日経クロステック Xtech
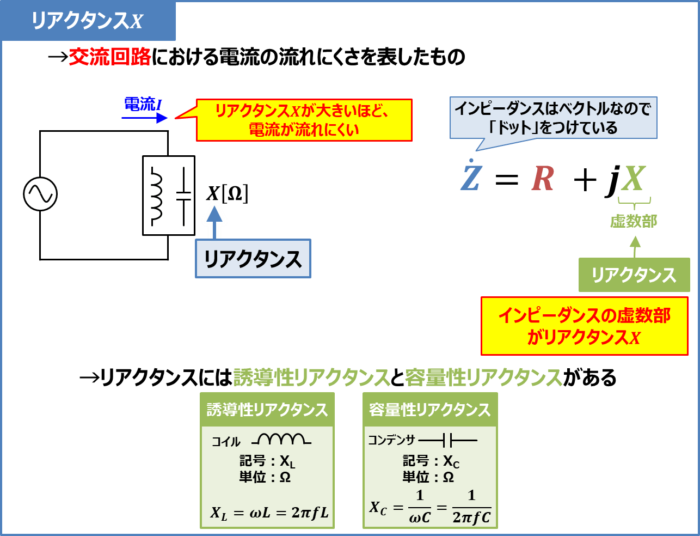
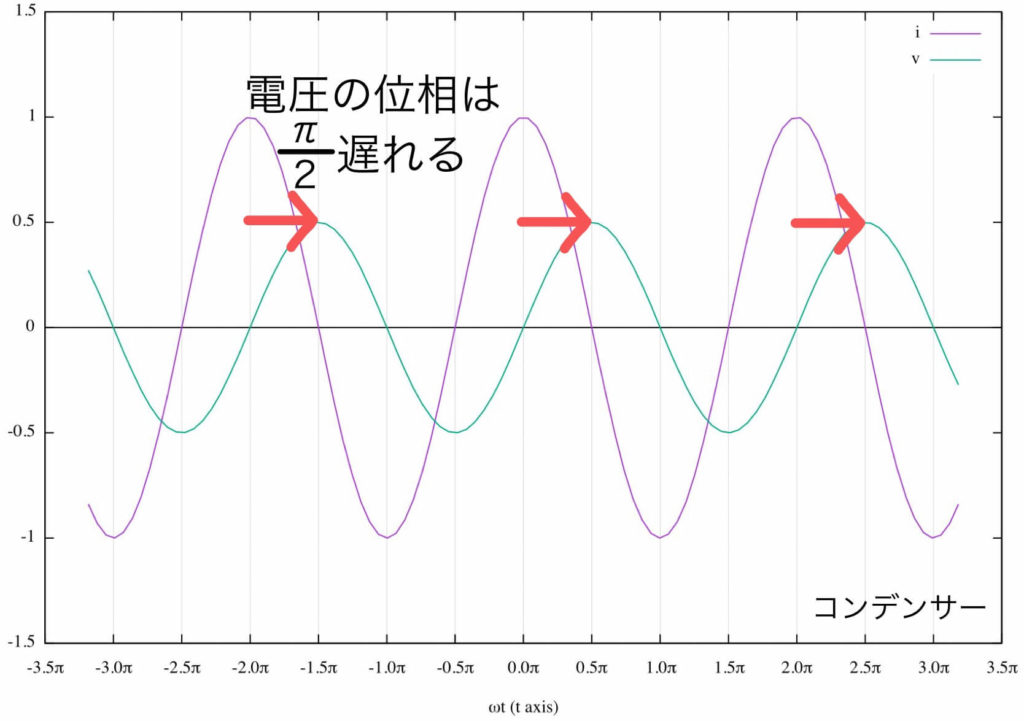
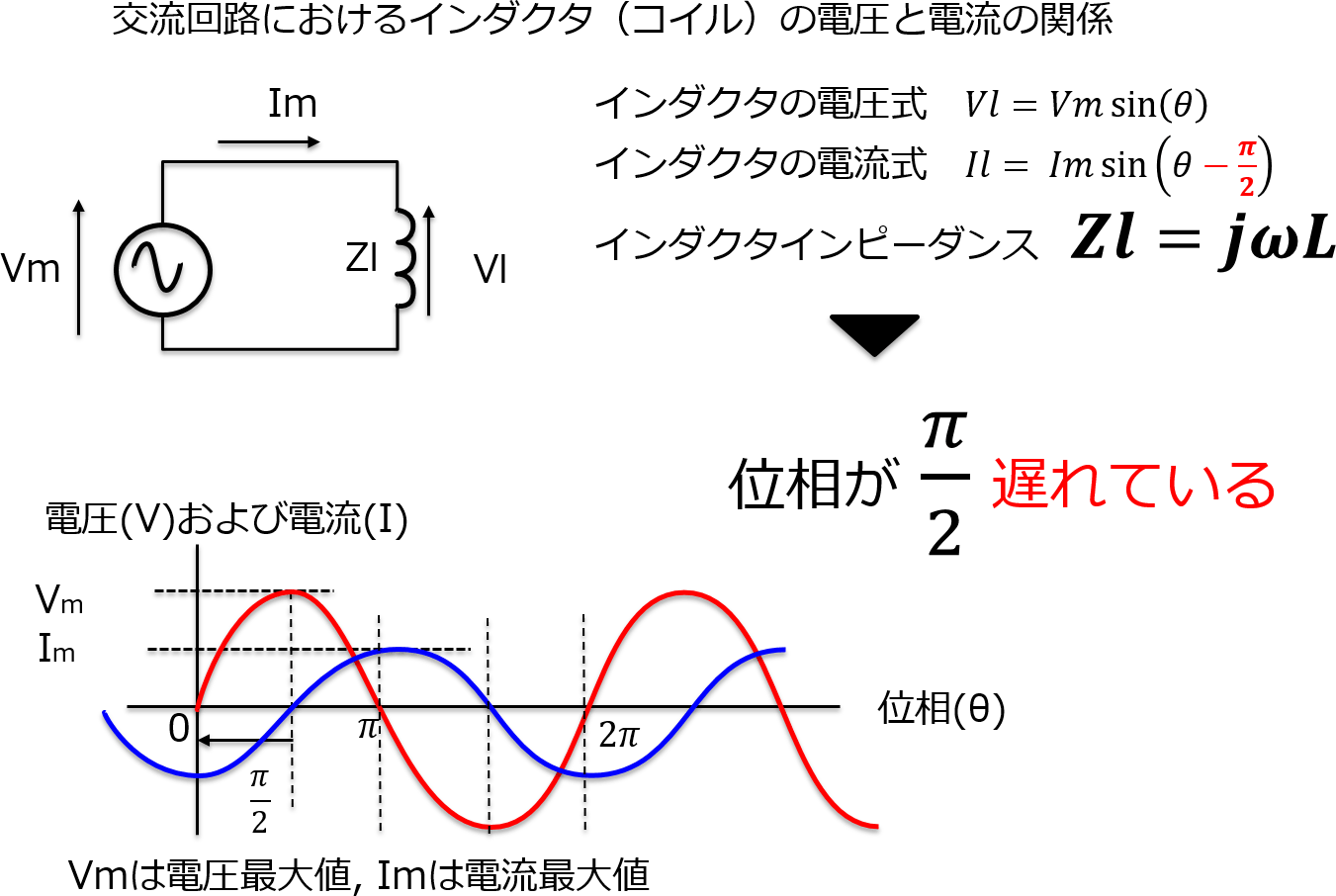
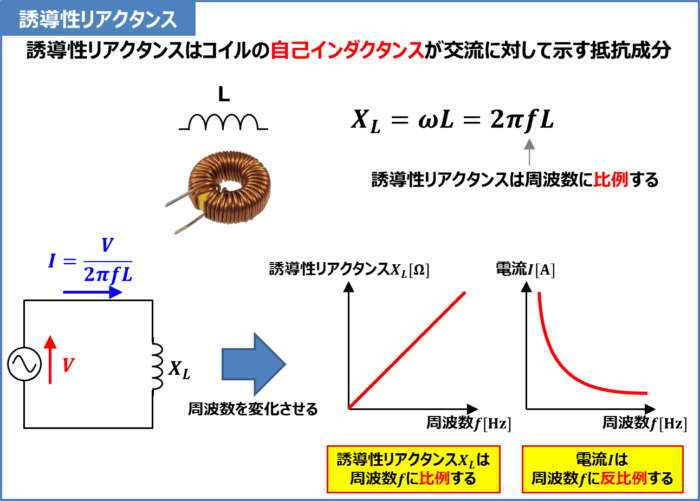
電流と電圧の関係 実効値の話を思い出してください。 抵抗に直流電圧を加えたときと，同じ実効値の交流電圧を加えたときでは，流れる電流は等しくなります。 ところが，抵抗とコイルを直列接続した場合，流れる電流は交流のほうが小さくなります！電流を妨げる大きさを表わすもの でしたので、コイルのリアクタンス（誘導性リアクタンス）を XL X L Ω Ω として回路図で書いてみると次のような意味になります。 式で書くと次のようになります。 ∴ XL = V I ∴ X L = V I Ω Ω この式を電流の式に コイルとコンデンサーの場合消費電力の時間平均は0ですから、基本的にコイルやコンデンサーでは電力を消費しません。 コイルの電圧の位相は電流に比べて $\dfrac{\pi}{2}$ 進んでいます（いいかれば、電流の位相は電圧に比べて $\dfrac{\pi}{2}$ 遅れています
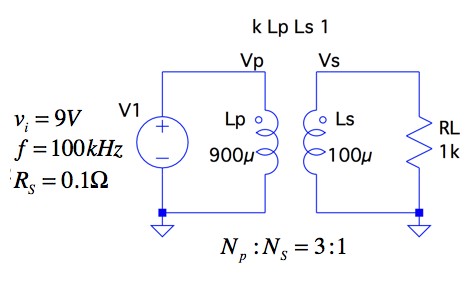
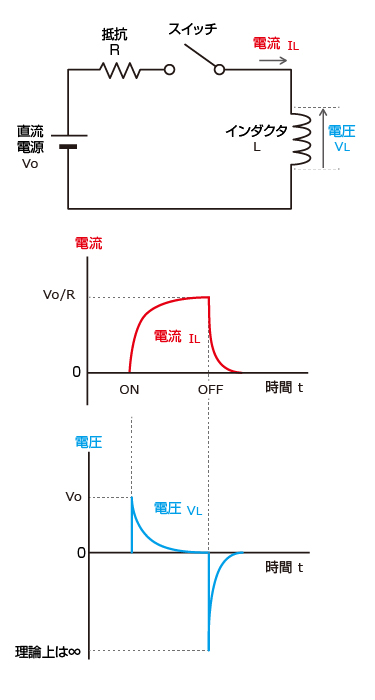
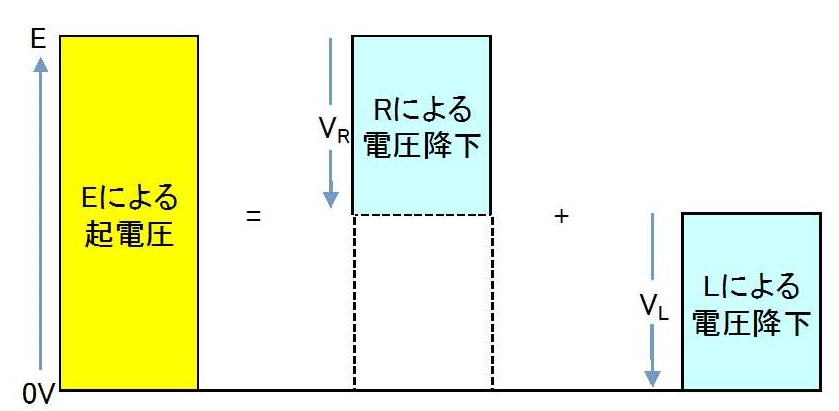
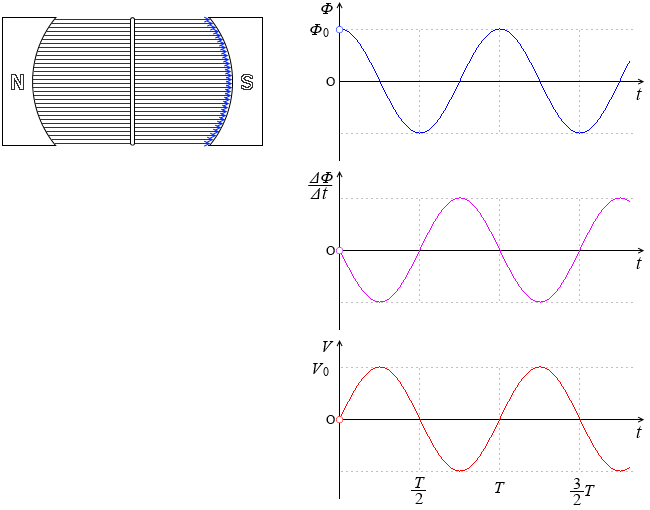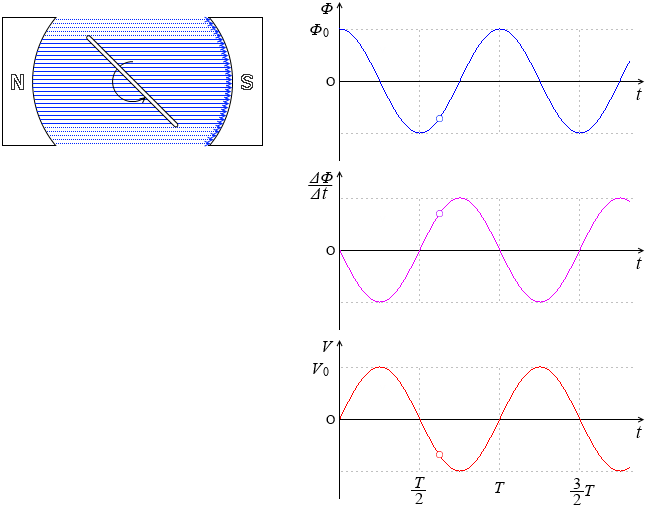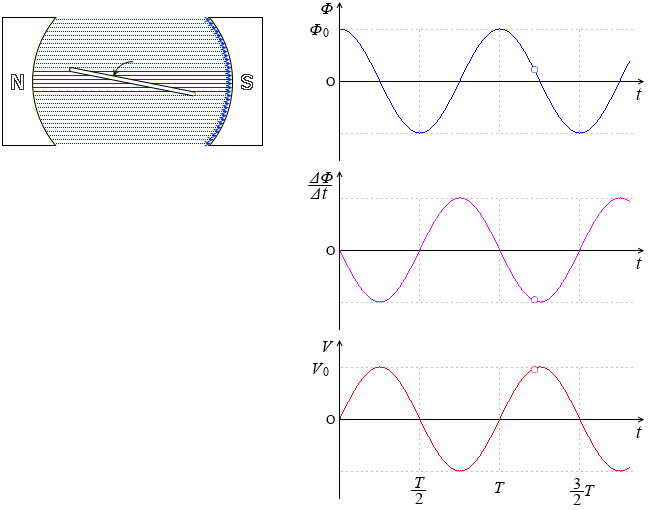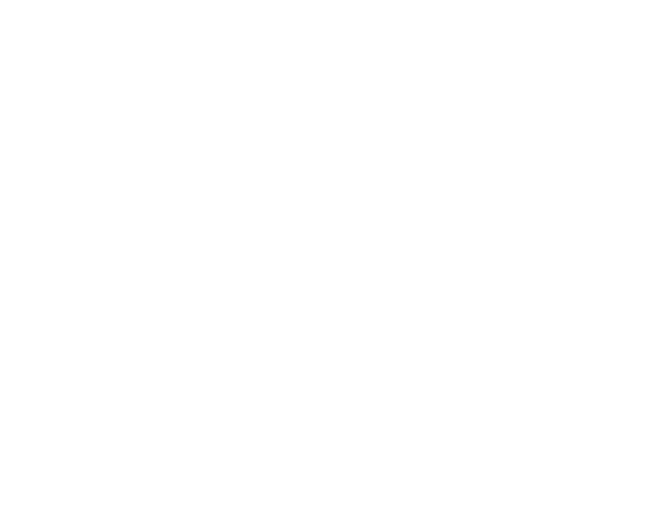
抵抗とコイルを直列に接続したRL直列回路について、電圧、電流、インピーダンスの関係について説明します。 RL直列回路とRC直列回路の考え方は、コイルとコンデンサの違いだけで基本的には同じです。 目次 RL直列回路の概要 RL直列回路のベクトル図 RL②にて、電圧は0を過ぎ、逆向きの電圧がかかり始め、 電圧が①と逆向きに最大値を取る時、①と同様自己誘導の関係から、電流値が0となります 。 ・・・・ という、 電圧が先に動き、電流が追いかける という流れが、コイルに交流を流すと繰り返され、コイルの充電・放電過程 充電・放電時の, コイルの端子間電圧, コイルを流れる電流, コイルの蓄えるエネルギーは下図のように時間変化する 指数関数 e − 1 τ t における τ (タウ)を時定数といい, 指数関数的に変化する物理量の変化速度の指標として用い
コイル 電圧 公式のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
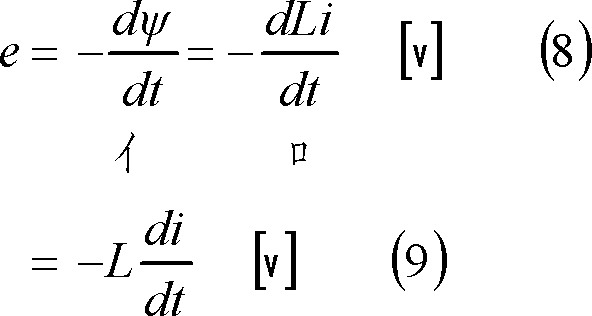 コイルに交流を流すと インダクタンス |  コイルに交流を流すと インダクタンス | 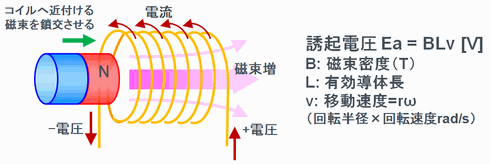 コイルに交流を流すと インダクタンス |
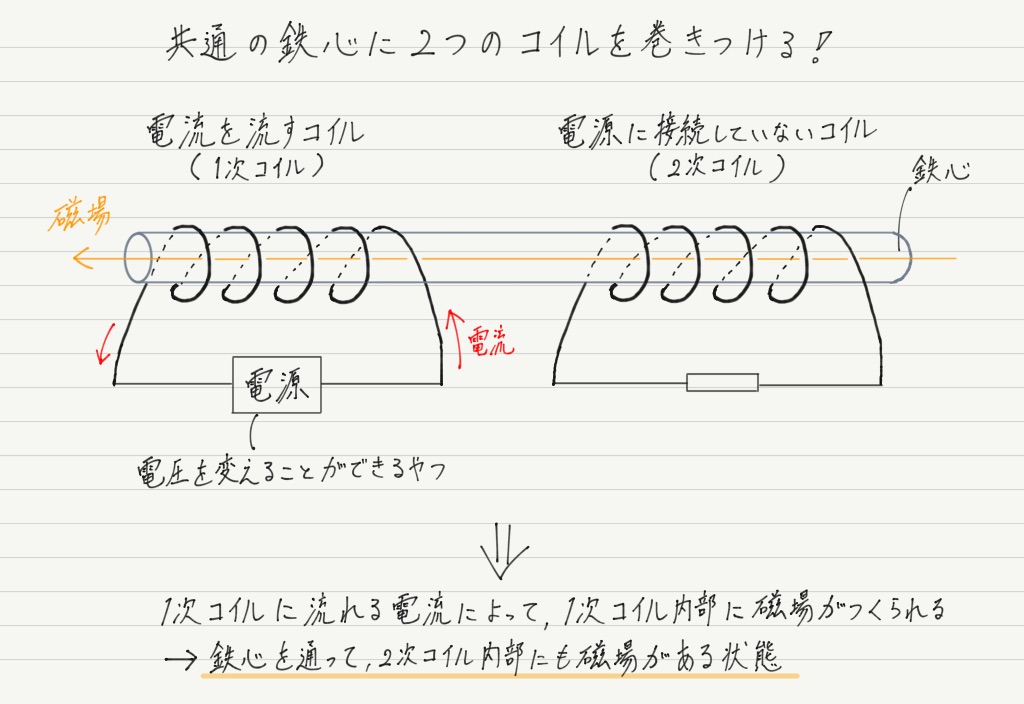コイルに交流を流すと インダクタンス |  コイルに交流を流すと インダクタンス |  コイルに交流を流すと インダクタンス |
 コイルに交流を流すと インダクタンス | 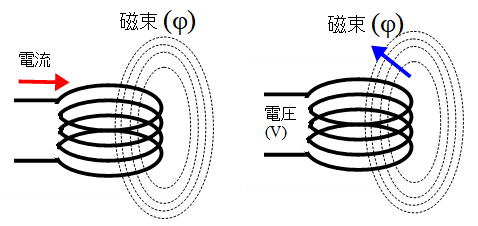コイルに交流を流すと インダクタンス |  コイルに交流を流すと インダクタンス |
「コイル 電圧 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 コイルに交流を流すと インダクタンス |  コイルに交流を流すと インダクタンス |  コイルに交流を流すと インダクタンス |
 コイルに交流を流すと インダクタンス |  コイルに交流を流すと インダクタンス |  コイルに交流を流すと インダクタンス |
 コイルに交流を流すと インダクタンス |  コイルに交流を流すと インダクタンス |  コイルに交流を流すと インダクタンス |
「コイル 電圧 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
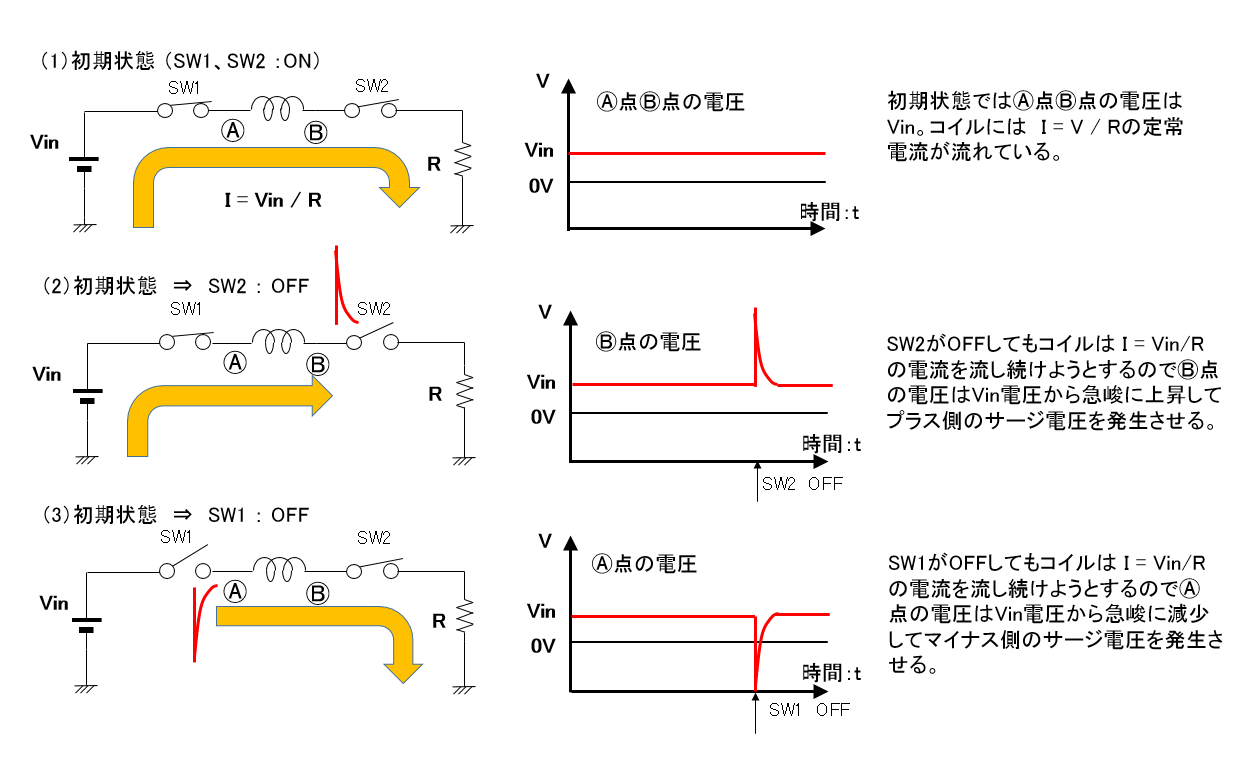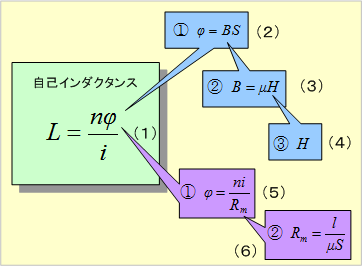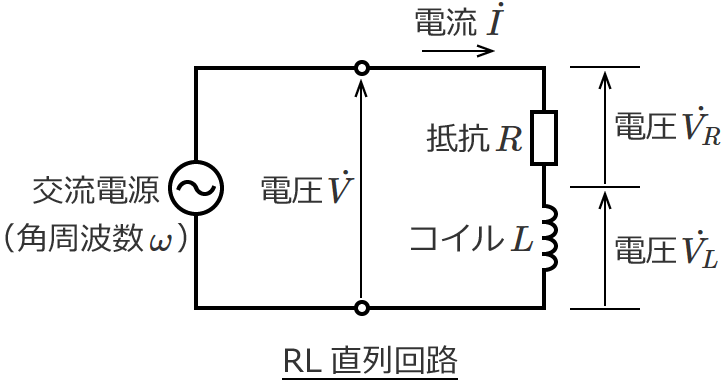 コイルに交流を流すと インダクタンス |  コイルに交流を流すと インダクタンス |  コイルに交流を流すと インダクタンス |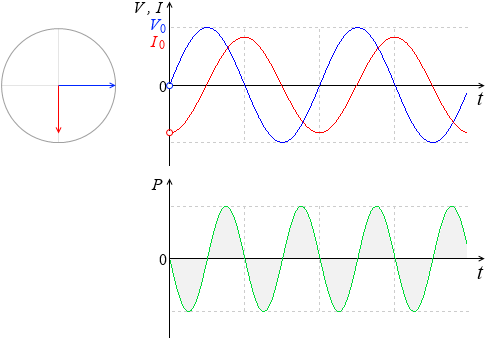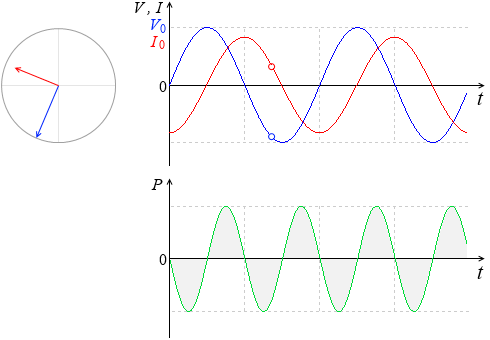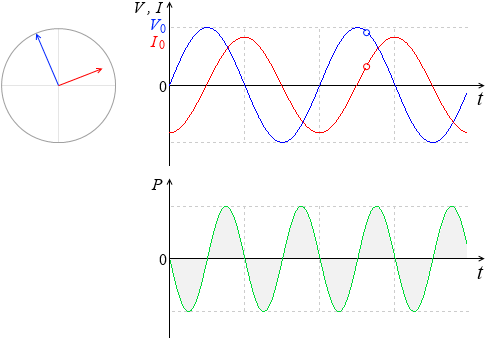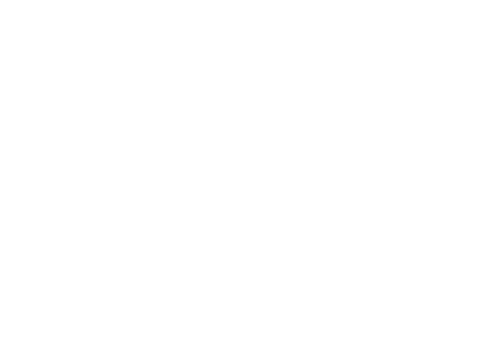
 コイルに交流を流すと インダクタンス |  コイルに交流を流すと インダクタンス |  コイルに交流を流すと インダクタンス |
 コイルに交流を流すと インダクタンス | 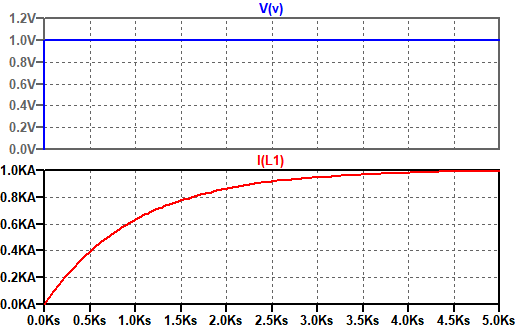 コイルに交流を流すと インダクタンス |  コイルに交流を流すと インダクタンス |
「コイル 電圧 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 コイルに交流を流すと インダクタンス | 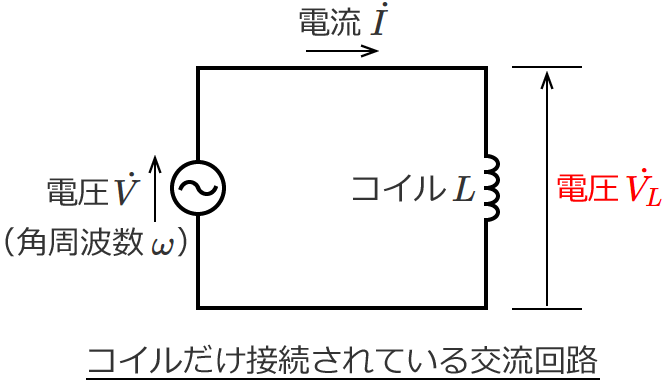 コイルに交流を流すと インダクタンス |  コイルに交流を流すと インダクタンス |
 コイルに交流を流すと インダクタンス |  コイルに交流を流すと インダクタンス | コイルに交流を流すと インダクタンス |
 コイルに交流を流すと インダクタンス |  コイルに交流を流すと インダクタンス |  コイルに交流を流すと インダクタンス |
「コイル 電圧 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 コイルに交流を流すと インダクタンス |  コイルに交流を流すと インダクタンス | 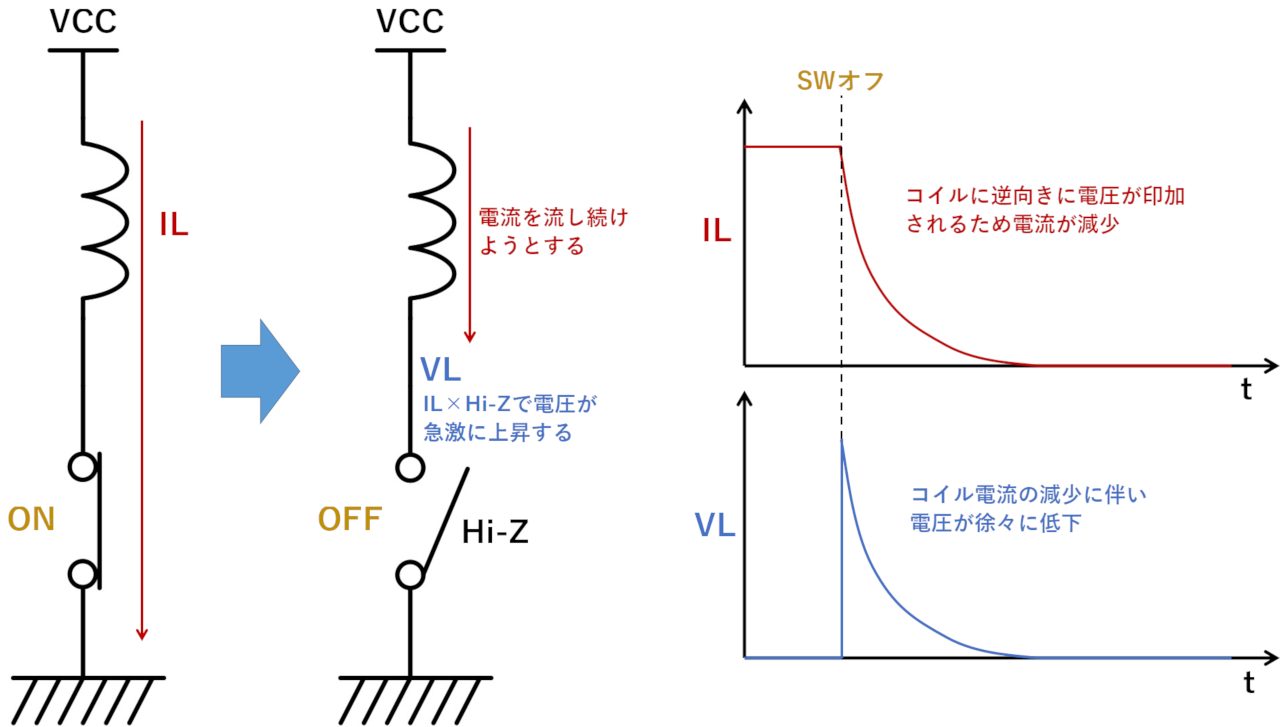 コイルに交流を流すと インダクタンス |
 コイルに交流を流すと インダクタンス | 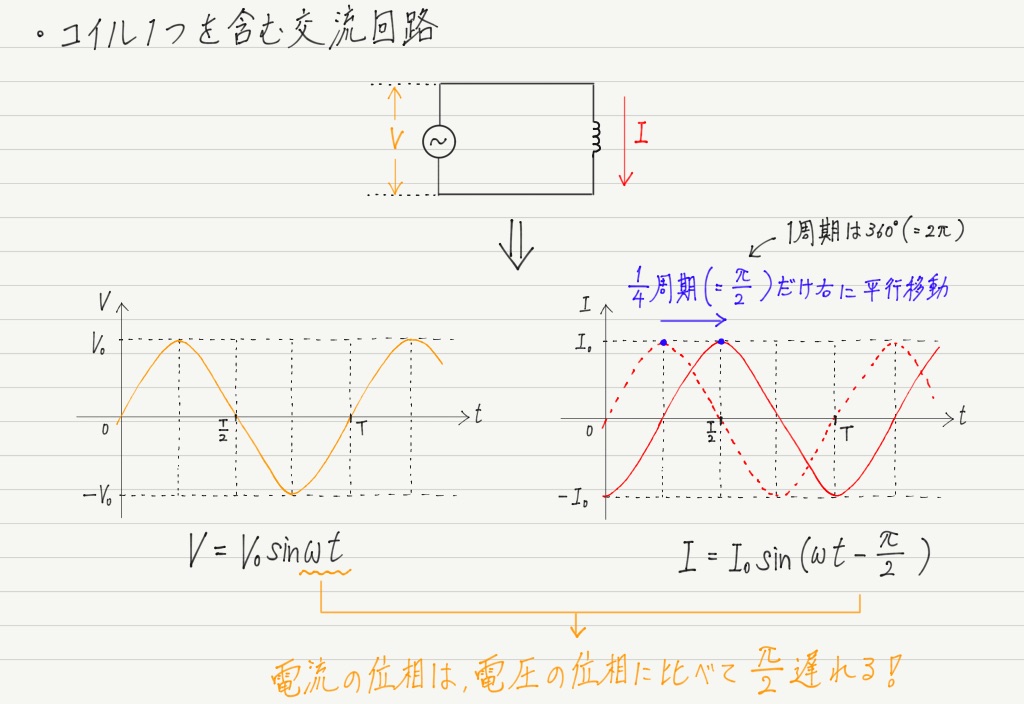 コイルに交流を流すと インダクタンス | 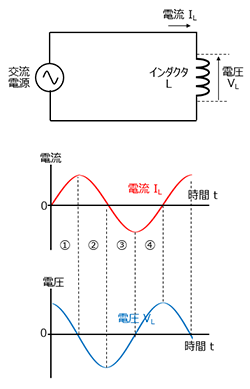 コイルに交流を流すと インダクタンス |
 コイルに交流を流すと インダクタンス | 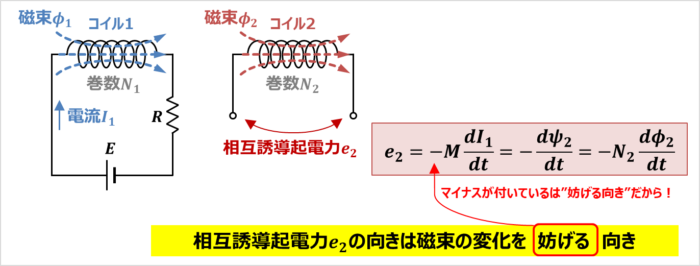 コイルに交流を流すと インダクタンス |  コイルに交流を流すと インダクタンス |
「コイル 電圧 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
コイルに交流を流すと インダクタンス |  コイルに交流を流すと インダクタンス |  コイルに交流を流すと インダクタンス |
 コイルに交流を流すと インダクタンス | 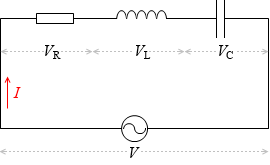 コイルに交流を流すと インダクタンス |  コイルに交流を流すと インダクタンス |
 コイルに交流を流すと インダクタンス | 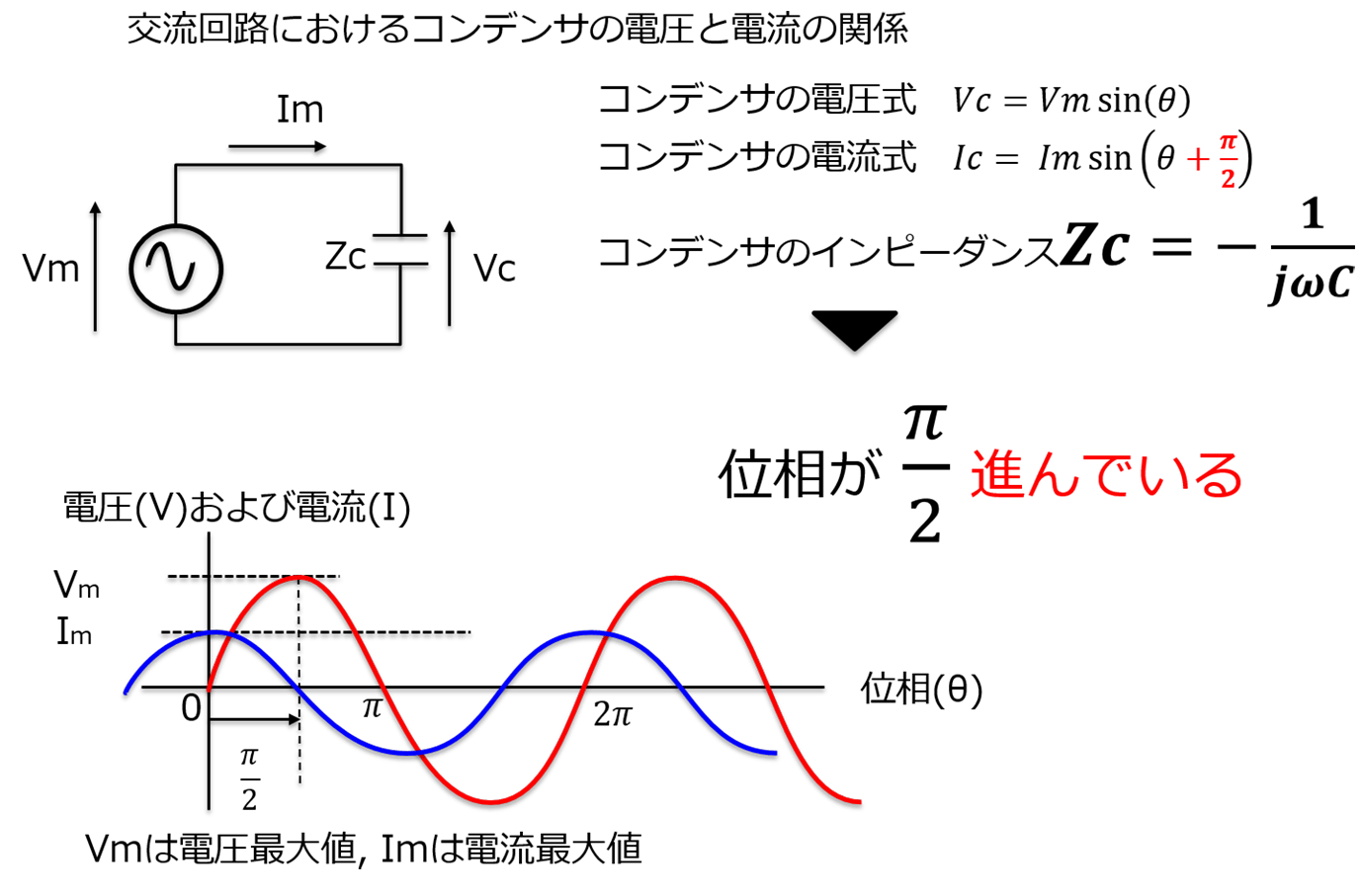 コイルに交流を流すと インダクタンス |  コイルに交流を流すと インダクタンス |
「コイル 電圧 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 コイルに交流を流すと インダクタンス |  コイルに交流を流すと インダクタンス |  コイルに交流を流すと インダクタンス |
 コイルに交流を流すと インダクタンス | 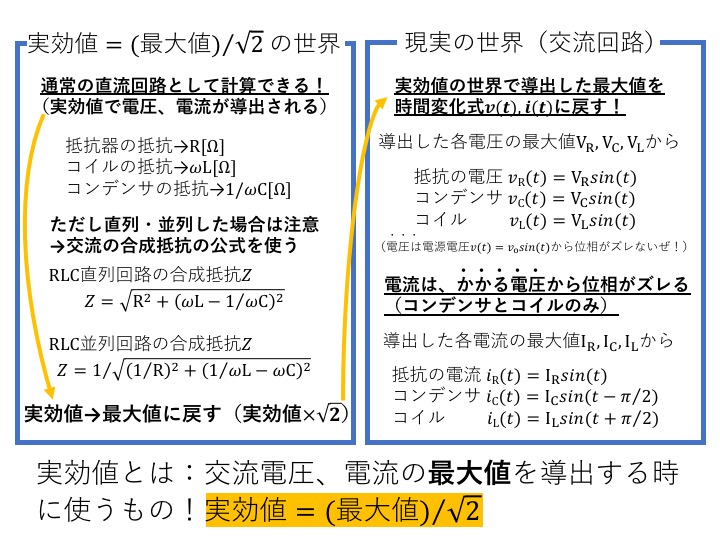 コイルに交流を流すと インダクタンス |  コイルに交流を流すと インダクタンス |
 コイルに交流を流すと インダクタンス |  コイルに交流を流すと インダクタンス | 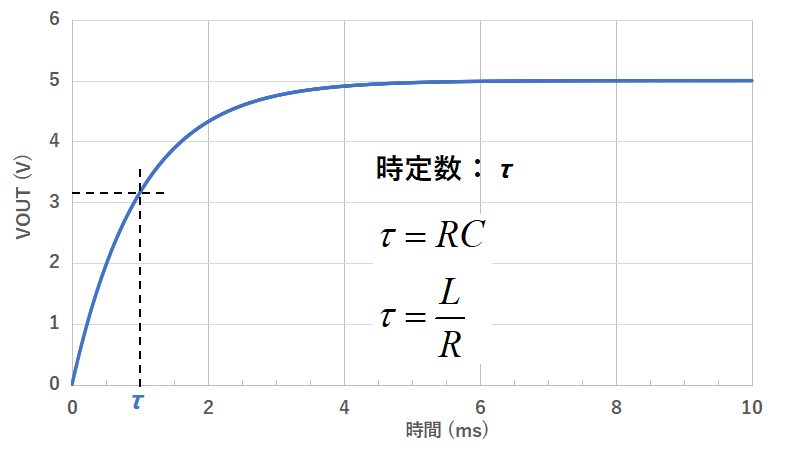 コイルに交流を流すと インダクタンス |
「コイル 電圧 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 コイルに交流を流すと インダクタンス | コイルに交流を流すと インダクタンス | 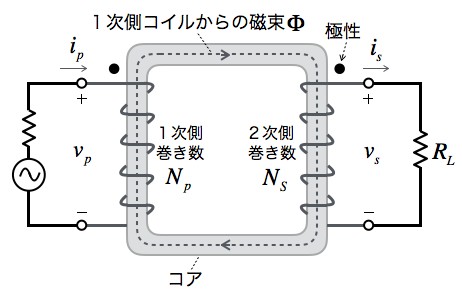 コイルに交流を流すと インダクタンス |
 コイルに交流を流すと インダクタンス |  コイルに交流を流すと インダクタンス |  コイルに交流を流すと インダクタンス |
 コイルに交流を流すと インダクタンス | 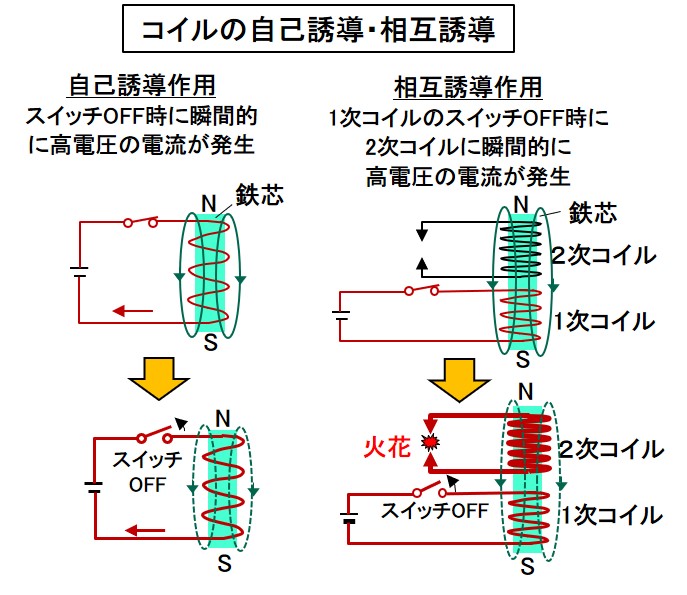 コイルに交流を流すと インダクタンス |  コイルに交流を流すと インダクタンス |
「コイル 電圧 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
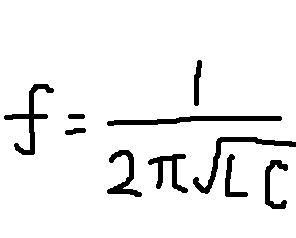 コイルに交流を流すと インダクタンス |  コイルに交流を流すと インダクタンス |  コイルに交流を流すと インダクタンス |
 コイルに交流を流すと インダクタンス | 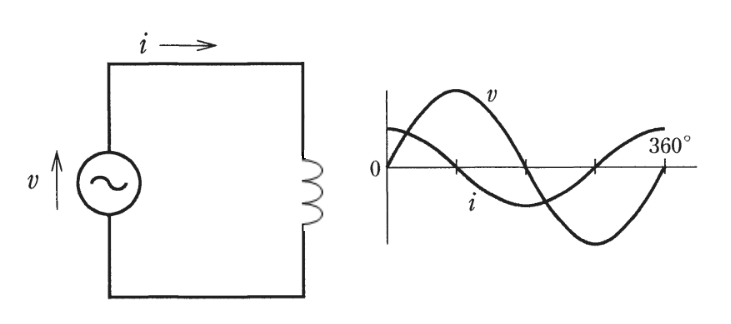 コイルに交流を流すと インダクタンス | 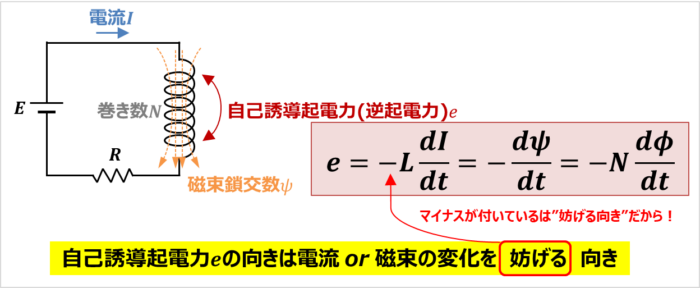 コイルに交流を流すと インダクタンス |
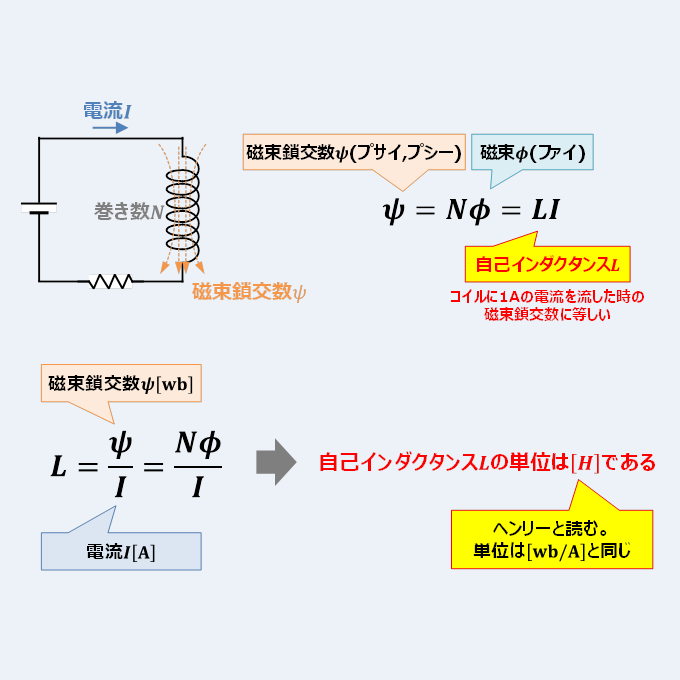 コイルに交流を流すと インダクタンス |  コイルに交流を流すと インダクタンス | 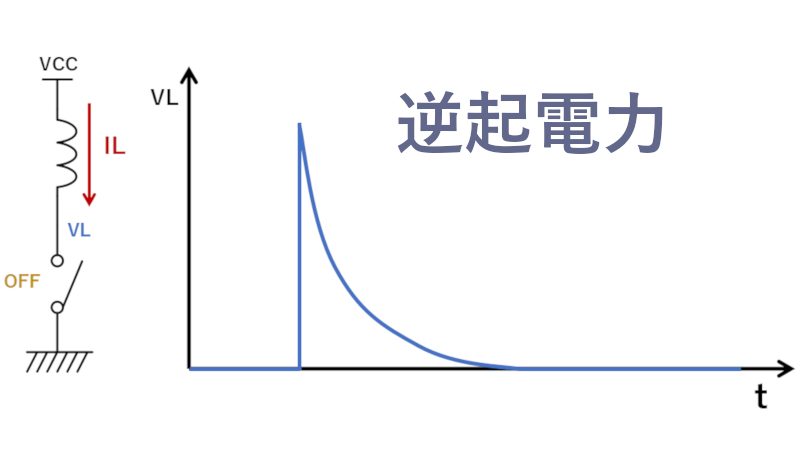 コイルに交流を流すと インダクタンス |
「コイル 電圧 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 コイルに交流を流すと インダクタンス | 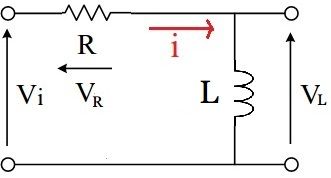 コイルに交流を流すと インダクタンス |  コイルに交流を流すと インダクタンス |
 コイルに交流を流すと インダクタンス |  コイルに交流を流すと インダクタンス |  コイルに交流を流すと インダクタンス |
 コイルに交流を流すと インダクタンス | コイルに交流を流すと インダクタンス | 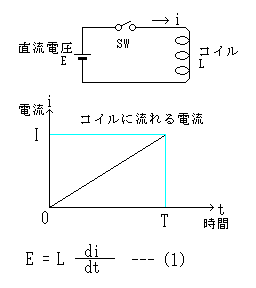 コイルに交流を流すと インダクタンス |
「コイル 電圧 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 コイルに交流を流すと インダクタンス | 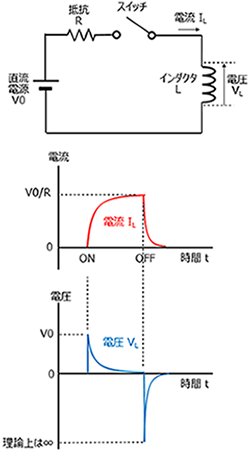 コイルに交流を流すと インダクタンス | 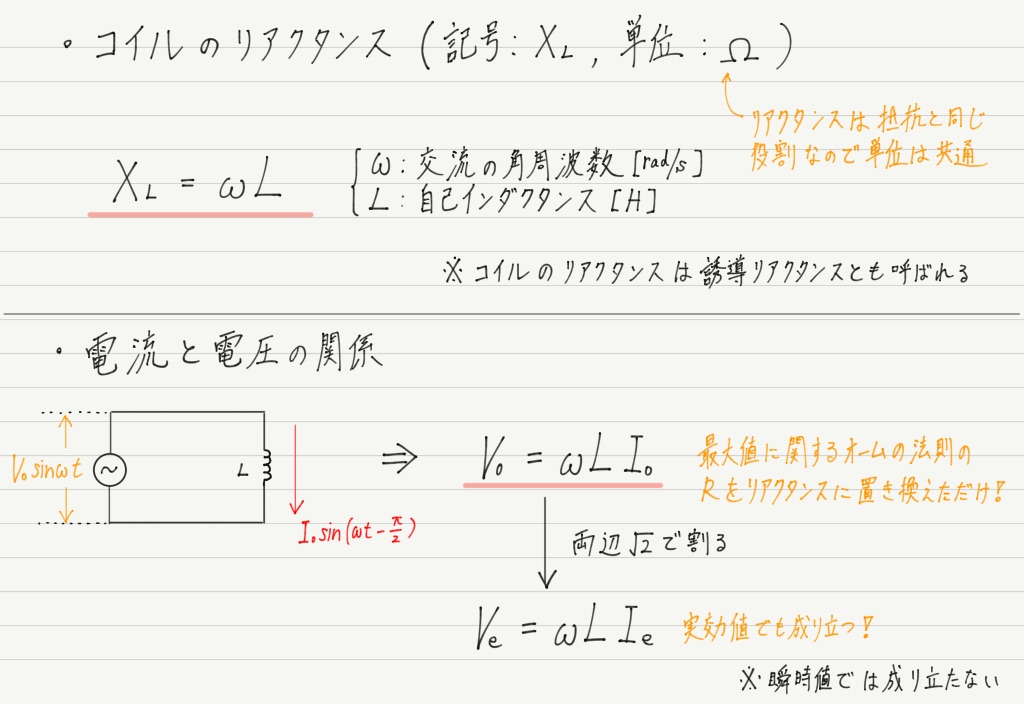 コイルに交流を流すと インダクタンス |
 コイルに交流を流すと インダクタンス | 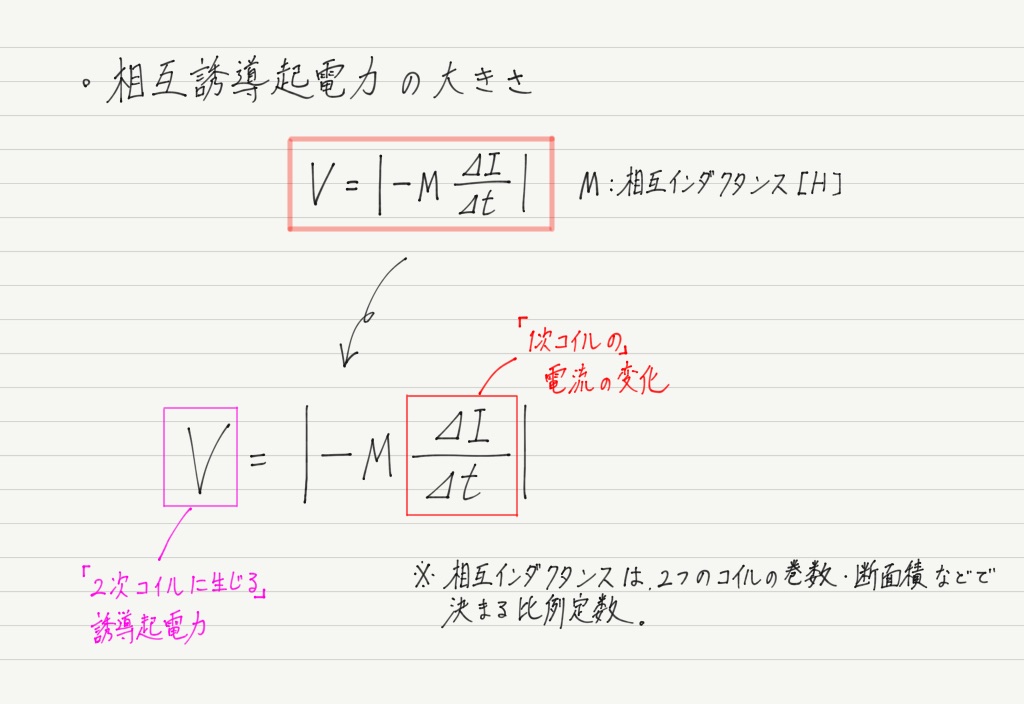 コイルに交流を流すと インダクタンス |  コイルに交流を流すと インダクタンス |
 コイルに交流を流すと インダクタンス |  コイルに交流を流すと インダクタンス | 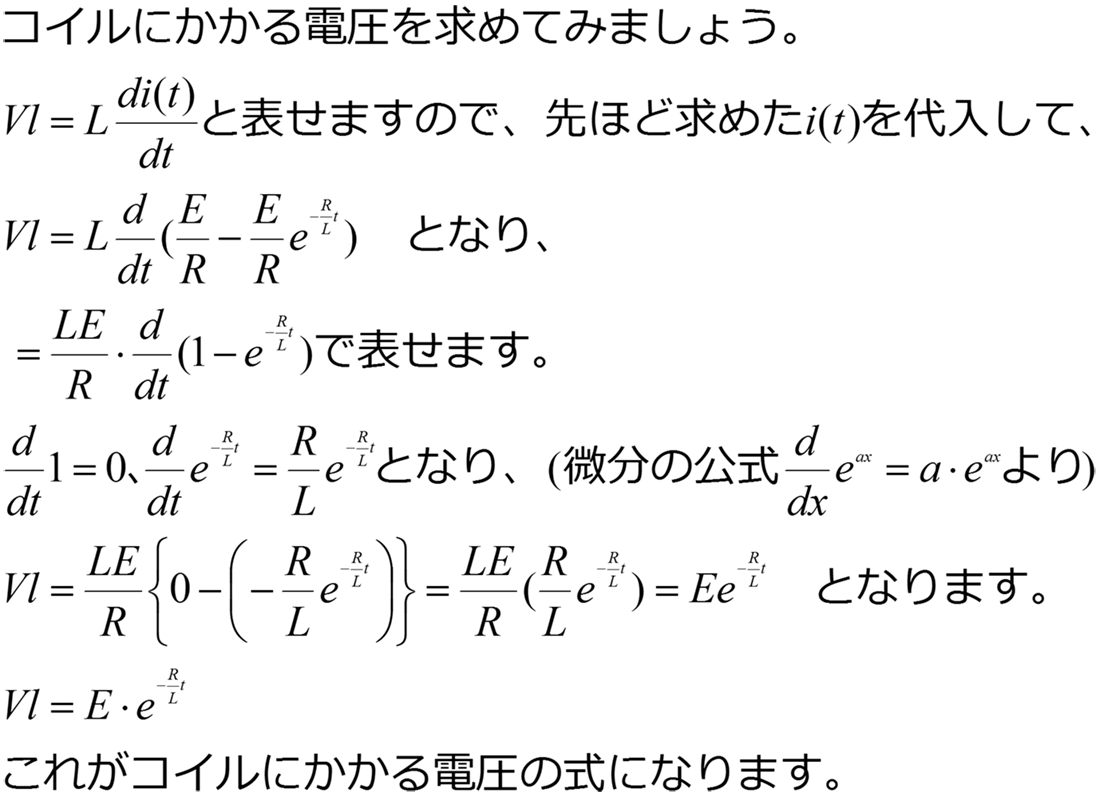 コイルに交流を流すと インダクタンス |
「コイル 電圧 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 コイルに交流を流すと インダクタンス | 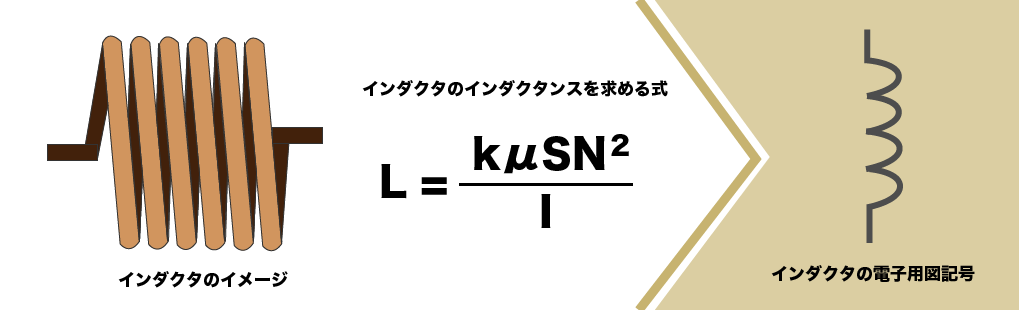 コイルに交流を流すと インダクタンス |  コイルに交流を流すと インダクタンス |
 コイルに交流を流すと インダクタンス | 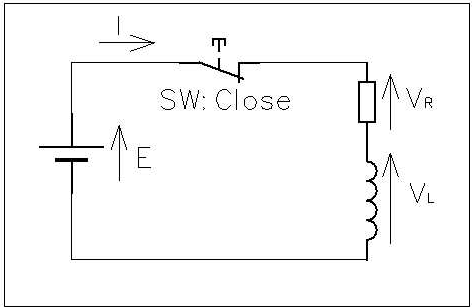 コイルに交流を流すと インダクタンス |
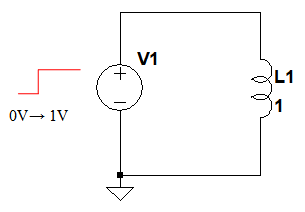
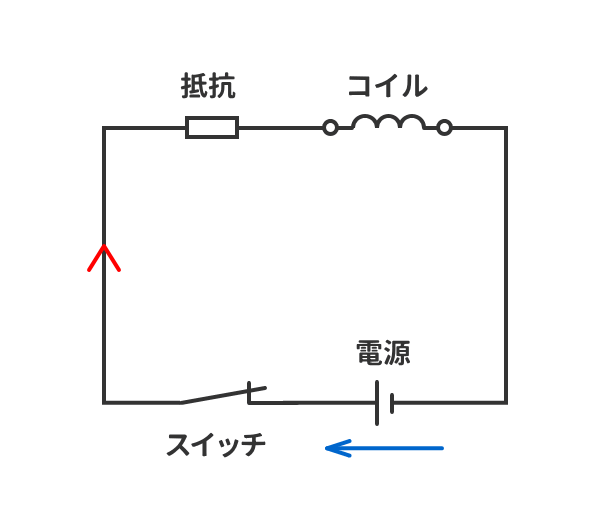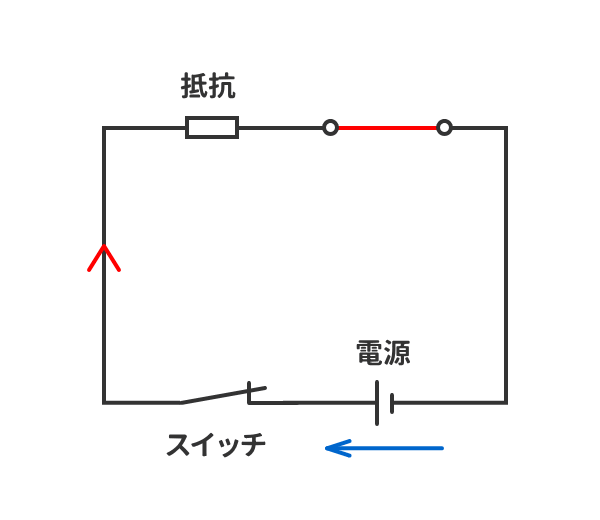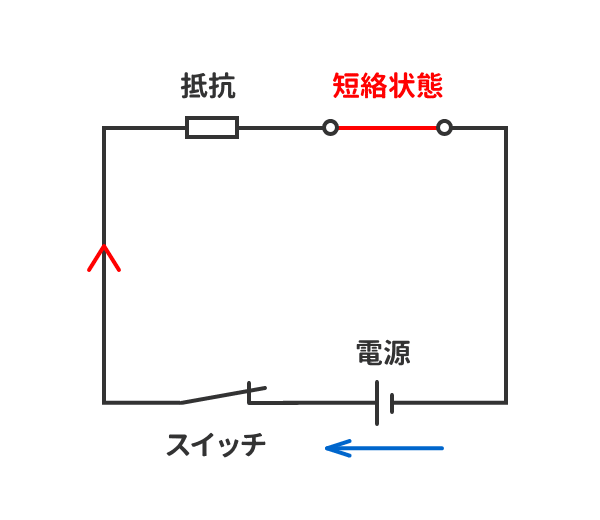
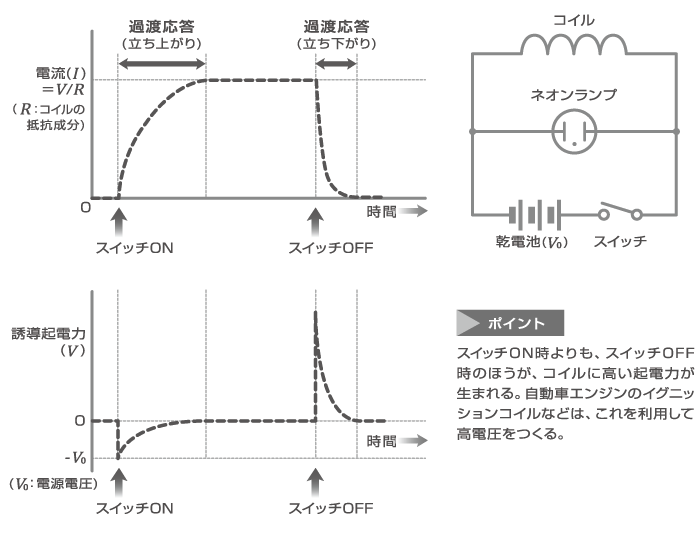
コイルに直流電圧を印加したときコイルの両端電圧 は0ですと言う意味に取れる解説をしている本を見かけることがあります。 本当にコイルに直流電圧を印加するとコイルの電圧は0なんでしょうか？ 少し詳しくみてみましょう。 しかし、コイルは電流の変化を妨げる方向に電圧を発生させます。 その結果、コイルとスイッチ（抵抗）の間の電圧が跳ね上がり、その電圧値は式 (1)になります。 前回の結果 を式 (1)に代入してグラフ化してみました。 スイッチをOFFにして抵抗値が
Incoming Term: コイル 電圧 公式,
0 件のコメント:
コメントを投稿